 |
| A Diagram of the Sun showing the Photon Random Walk |
We can see that the actual displacement is the sum of the vectors of each individual step. In order to put this into a scalar quantity, we take the dot product of displacement. This dot product can be rewritten in terms of the cosine of the angle between the vectors.
\[N\:=\:(\frac{\Delta r}{l})^{2}\]
The diffusion velocity is how fast the photon is effectively traveling over a large displacement \(\Delta r\), usually from the core to the surface. Although the photon is always traveling at the speed of light, its random walk path makes its velocity relative to the total displacement much less than the speed of light.
The total time it takes to travel every single step is thus equal to \(\frac{N\:\times\:l}{c}\), where \(N\)is the number of steps, \(l\) is the length of each step (mean free path), and \(c\) is the speed of light. We can then divide \(\Delta r\) by the total time in order to get the diffusion velocity:
\[v_{diff}\:=\:\frac{c}{N^{\frac{1}{2}}}\]
We can represent the photon's path over a specific region leading up to a collision with a diagram. At the beginning of the step, the photon is situated a distance \(l\) away from the electron that it will collide with. Since there is only one electron in this specific region, the number density is \(\frac{1}{volume}\). We can then express the mean free path, \(l\) in terms of the number density and the electron's cross-sectional area.
Using our definitions for these terms and our original definition of diffusion velocity, we can do some substitutions, namely with \(l\), in order to come up with an expression for diffusion velocity in terms of \(\kappa\) and \(\rho\).
\[N\:=\:(\frac{\Delta r}{l})^{2}\]
\[N^{\frac{1}{2}}\:=\:\frac{\Delta r}{\frac{1}{\kappa \rho}}\:=\:\Delta r \kappa \rho\]
Thus, the diffusion velocity can be written as:
\[v_{diff}\:=\:\frac{c}{\Delta r \kappa \rho}\]
Now that we have determined the diffusion velocity, we can approach easily approach this problem. The diffusion velocity helps us understand how quickly a photon can move over a total displacement. In this case, that total displacement, \(\Delta r\) is the radius of the Sun. We have already developed the expressions to solve for the total time. Now all we have to do is plug in the specific values which are listed below:
We can then use this to solve for the diffusion velocity. Finally, we can plug into our equation for total time, \(\frac{\Delta r}{v_{diff}}\) and we have solved for the time scale.

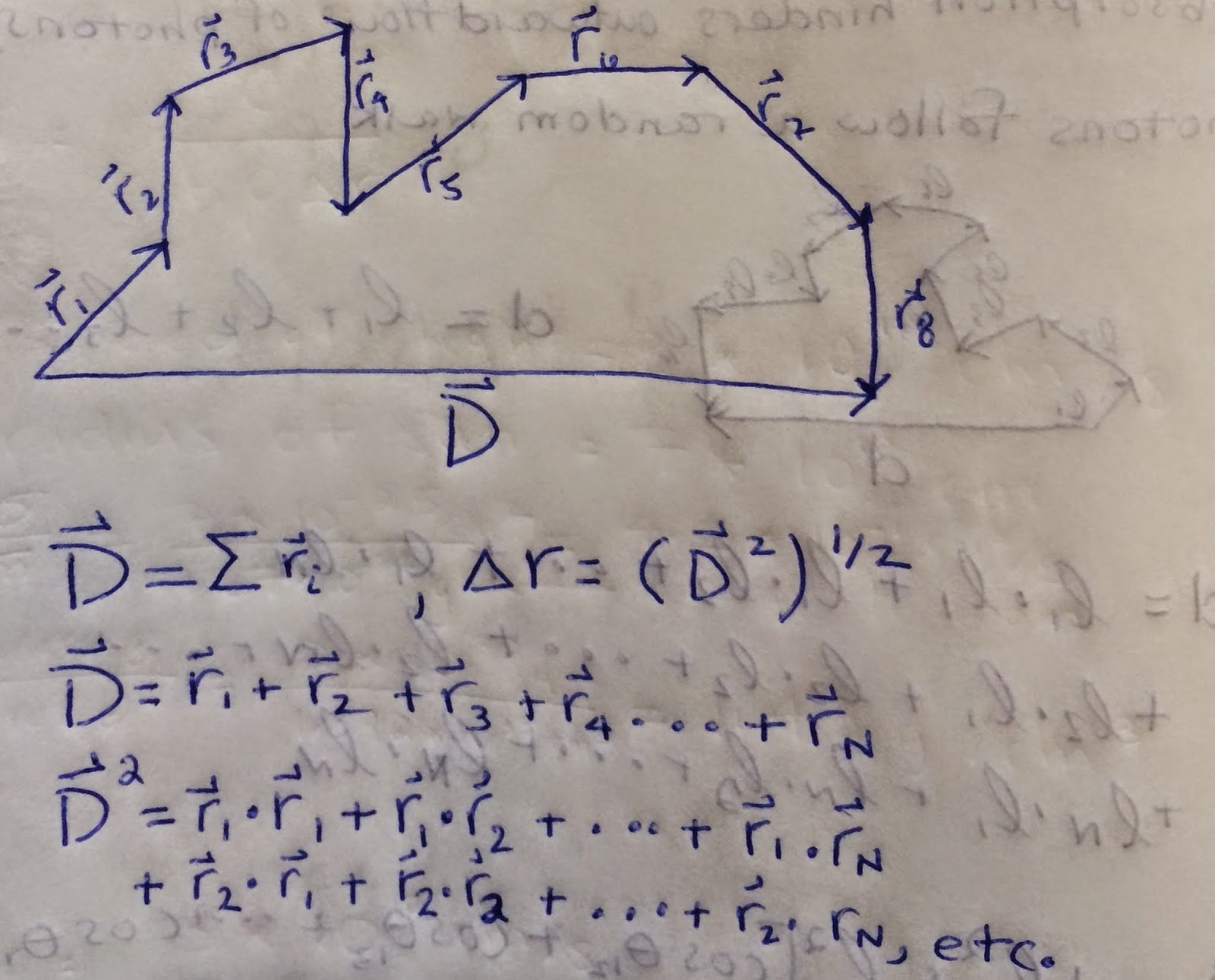









Very nice work, Carter! In the last step, be sure that you're using the "expert method", and solving for the time in terms of variables, only substituting at the very end.
ReplyDeleteThanks for the advice Benjamin. I suppose the way I structured this, I solved for Vdiff first and then solved for time. I should have put my expression for time at the top and then worked from there so I would have all the variables before solving for Vdiff. I'll be sure to stick to the expert method in the future!
Delete